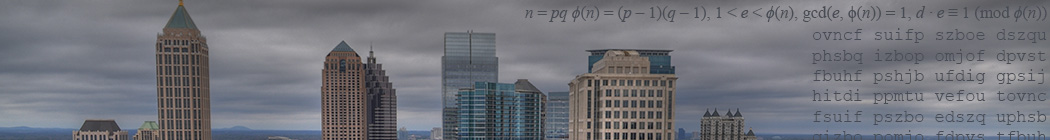A practical application of the EA is computing solutions to linear equations: the videos on this page will demonstrate how to do so, and provide a proof that our approach works, and explore this application with some examples.
Integer Solutions to a Linear Equation in Two Variables
Given two positive integers a and b, what is the minimum positive value of ax + by as x and y vary over all integers? The video shows us how we can do so, by applying the Euclidean algorithm backwards, and identifies the connection between the solution and a particular GCD.
A Second Example
To help convince ourselves that we have found a method that always finds that the smallest positive value of ax + by, let’s consider one more example.
Regarding the Computational Procedure
The approach we introduced (to finding an integer solution to a linear equation) is something that helps build an understanding of why the solution is what it is. If you are interested in writing a program that calculates the smallest integer solution to a linear equation, you can find one way to do so in the textbook.
[previous] [next]