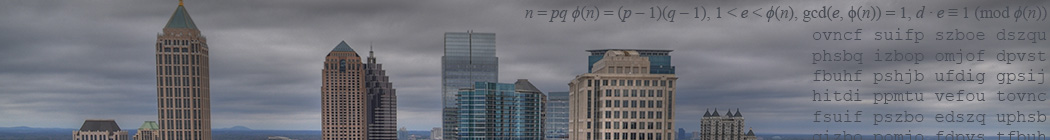Some of the fun and interesting applications that we will explore throughout this course are described in the following set of videos.
What is Number Theory?
So what is number theory all about? In this course, we will be interested in properties of integers and their applications. This video explores how some of these properties are applied in this course to divisibility and cryptography.
Casting Out Nines
Although number theory can be applied to many bases, we will only use numbers in base 10. The casting out nines algorithm, which is useful for giving us a quick approach to determining whether any given integer is a multiple of nine, depends on arithmetic in base 10.
A Prime Number Theorem and Cryptography
If we choose any positive integer, x, there is a useful theorem that tells us now many prime numbers are less than x. We will apply this theorem to cryptography, and encounter a surprising connection to the number e.
Knowing Whether a Given Number is Prime
Another application that we will explore in this class is to determine whether a given number is prime.
Relatively Prime Numbers and π
Other applications we will explore in this class involve relatively prime numbers. Surprisingly, if we were to choose two random integers, the probability that they are relatively prime is related to the number π.
Public Key Cryptography
Traditional cryptography depends on establishing a common secret, in advance.
Calendar Calculations
Modular arithmetic, a concept we explore in a few lessons, can be used to quickly calculate the day of the week that a given day falls on.
[previous] [next]